气象测量应用方向：石英晶体微天平理论与校准

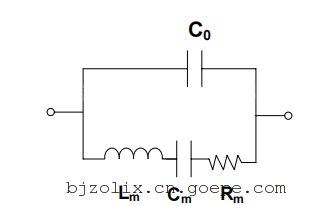
背景

Sauerbrey ¹ 是*一个认识到石英晶体微天平(QCM)技术潜在用途的人，并证明了这些压电器件对 QCM 电极表面质量变化的极其敏感的性质。他的研究结果体现在 Sauerbrey 方程中，该方程将QCM 电极表面单位面积的质量变化与观察到的晶体振荡频率的变化联系起来：f = - C_f .m (equation 1)

其中，

f-观察到的频率变化，以 Hz 为单位，

m-单位面积质量变化，以 g/cm² 为单位，C _f -所用晶体的灵敏度系数（即 56.6 Hz g ^-1 cm² 用于室温下 5MHz AT-cut 石英晶体）。

Sauerbrey 方程依赖于线性灵敏度系数 C _f ，这是 QCM 晶体的一个基本特性。因此，在理论上，QCM 质传感器不需要校准。然而，必须记住的是，Sauerbrey 方程只严格适用于均匀的、刚性的、薄膜沉积² 。真空和气相薄膜沉积不能满足这些条件，实际上表现出更复杂的频率-质量相关性，通常需要一些校准才能得到准确的结果。多年来，QCM 一直被认为是气相质量探测器；然而，*近，随着科学家们意识到它们可以与液体和粘弹性沉积物接触，使得它们的应用得到了扩展。在这种情况下，石英振荡器的频率和串联谐振电阻对于完*表征与晶体电极接触的材料是非常重要的。用于流体的 QCM 开发开辟了一个新的应用领域，包括电化学和微流变学。*近的发挥在那集中在定制电极表面化学（即专门的聚合物涂层），以便这些设备可以被应用于(1)特定气体检测，(2)环境监测，(3)生物传感，(4)基本表面分子相互作用研究的鉴别质量检测器。

本章的目的是为QCM用户提供不同的测量和校准技术的简要介绍，并简要描述用于解释结果的、*常用的理论模型。对这些主题的全面讨论显然超出了本说明的范围。然而，从真空薄膜沉积到电化学实验中，已经发表了许多关于 QCM 的操作和校准的文章，QCM 用户可以参考本章末尾的出版物列表以获得更详细的信息。

QCM 振荡器

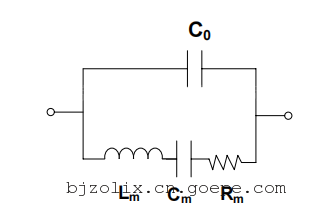
石英晶体谐振器的 Butterworth van Dyke（BVD）电学模型³ 如图 1 所示。该模型常用于表示晶体谐振器在接近串联谐振时的电学行为，该模型在预测 AT-cut 石英晶体在 QCM 应用中的频移和损耗方面也很有用。

图 1：石英晶体谐振器的 Butterworth van Dyke 模型。

BVD 电模型由两条电路组成。运动臂具有三个系列组件，由晶体的质量和粘性载荷修改：(1)R _m（电阻）对应于安装结构和与晶体接触的介质的振荡能量耗散（即粘性溶液引起的损耗），(2)C _m（电容）对应于振荡中存储的能量，与石英和周围介质的弹性有关；(3)L _m（电感）对应于振荡的惯性分量，它与振动过程中位移的质量有关。对于 QCM 系统中使用的直径 1 英寸的 5MHz 晶体，这些参数的典型值为 C _m =33fF，L _m =30mH 和 R _m =10Ω（用于干晶体），R _m =400Ω（水中的晶体），或 R _m =3500Ω（88%甘油的晶体）。

运动臂由寄生电容 C _o 分流，C _o 表示晶体电极、支架和连接器电容的静态电容之和。在 QCM 系统₄ 中，C _o 约为 20pF，通过将电子器件直接放置在晶体支架上，从而消除电缆电容，从而保持了较小的值。

在 QCM 应用中，当质量增加到晶体电极时，运动电感 L m 增加——串联谐振的频移是增加质量的敏感指标，小于 1ng/cm 2 的薄膜可以很容易地通过 QCM 分辨出来。运动电阻 R _m也可以提供有关该过程的重要变量，因为软薄膜和粘性液体会增加运动损耗，从而增加 R _m 的值。

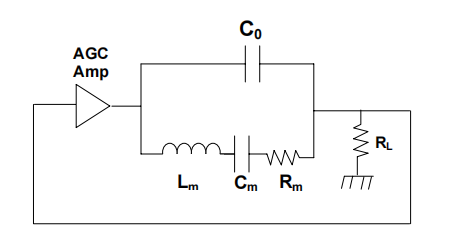
图 2.振荡器电路由 AGC 放大器、石英电阻器和负载电阻器组成。

将晶体放置在振荡器电路中提供了一种测量其运动参数的简单方法⁵ 。图 2 显示了 BVD 晶体模型，由自动增益控制放大器驱动（AGC），且端接负载电阻 R _L 。通过将 R _L 上的电压返回到 AGC 放大器的输入端，如果有足够的增益，电路将以环路周围相移为 0°（或 360°的整数倍）的频率振荡（Barkhausen准则）。如果没有C _o ，则很容易看出在C _m 和L _m 的串联谐振是(即f _SR = [ 1 / [2.Π .(L _m .C _m )^1/2 ])满足相位条件.在串联谐振时，C _m 和 L _m 的电抗抵消，只留下 R _m 。在这种情况下，一个值为 A _v =（R _m + R _L ）/ R _L 的放大器增益将提供 1 的环路增益来维持振荡。

不幸的是，C _o 在 QCM 应用中不能被忽略。在图 2 所示的电路中，C _o 向 R _L 注入超前电流，该超前电流必须通过运动臂被滞后电流抵消，以达到零相位条件。这需要电路运行在串联谐振至上，其中C _m 和 L _m 的净电抗是感应的。事实上，如果 R _m 足够大，运动臂可能无法提供足够的滞后电流来抵消通过 C _o 的超前电流，电路也可能根本不会振荡。

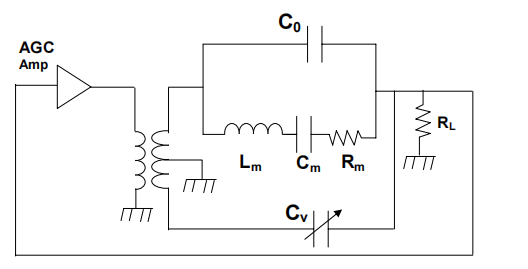
图 3.C ₀ 变零的振荡器电路。

图 3 显示了一种取消 C _o 的方法。在这个电路中，AGC 放大器驱动具有两个次级绕组的变压器。一个次级驱动晶体和负载像以前一样，而另一个则是次级反转电压。反转电压源通过可调电容器 C _v注入电流，以抵消通过 C _o 注入的电流。当可调电容等于 C _o 时，可以实现精确的抵消。在 SRS 的QCM25晶体控制器中，C _v 是一个变容器，通过找到维持振荡所需增益*小的偏置设置，使其等于C _o 。

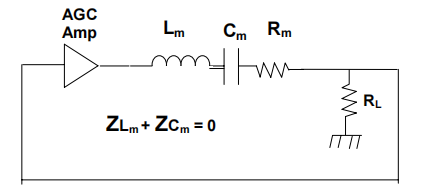
图 4.用 C _v 抵消 C ₀ 的振荡器电路模型。

在 C _o 取消后，电路简化为如图 4 所示。对于该电路，在 C _m 和 L _m 的电抗抵消的串联谐振中实现了零相位条件。在串联谐振时，R _m 和 R _L 形成一个电阻衰减器，需要 AGC 增益 A _v =（R _m + R _L ）/ R _L来维持振荡。通过了解维持振荡所需的 AGC 增益⁶ A _v ，我们可以确定 R _m = R _L .(A _v - 1)。

电容抵消

QCM 系统采用了一种零电容 C _o 的方法，以确保测量的频率和电阻值与石英振荡器的真实串联谐振参数相对应。

QCM 模拟控制器的前面板包括(1)十转表盘，以控制变容（C _v ）所需的偏置电压，(2)开关，用于将控制器设置为调整模式以进行零补偿。

有两种方法可以操作 QCM 模拟控制器在零 C _o 的串联谐振振荡。

C _o 中的单位间变化足够小，C _v 的可重复性足够好（±2pF），大多数用户可以将变容器偏置设置为一个固定值，从而忽略这个问题。将十转表盘设置为 5.0，这将为变容器提供 6.0 伏的反向偏置，使 C _v 约为 18pF。这种方法推荐用于 R _m 很低的“干燥”的应用，不推荐用于 R _m 可能很高的“粘性”的应用（如甘油溶液）。

带有电导锁定峰值检测电路的零电容 C _o 。在调整模式下，该单元将用 75Hz 正弦波调制变容偏置，并指示 C _o 共同补偿是高、低还是空为零。从十转表盘设置为 5.0 开始（LED 应指示晶体正在振荡），并切换到调整模式。如果高 LED“打开”，则降低表盘上的设置，如果低 LED“打开”，则增加设置，并将表盘锁定在两个空 LED 灯以相同强度发光的值范围的中间。完成后，将开关返回到 HOLD模式。

一般来说：

电容抵消对于精确测量液体和有损薄膜（即软膜）是*不可少的。

每次晶体环境发生改变时，都应检查并重新调整电容抵消。例如，当从空气过渡到液相时。

必须在实际测量环境中使用晶体 holder 和晶体进行抵消调整。

频率测量

QCM 提供了一个频率输出端口（BNC）。

实际上，任何商用的频率计数器都可以测量由 QCM 频率输出提供的 50Ω 中的 2.4Vpp 方波的频率，通过其计算机接口进行设置和读取计数器相对简单。

频率计数器的选择标准

针对 QCM 应用的频率计数器的选择标准包括：分辨率、速度、时基稳定性、计算机接口和软件驱动。需要仔细的选择，否则频率计数器可能会降低质量测量的测量结果。

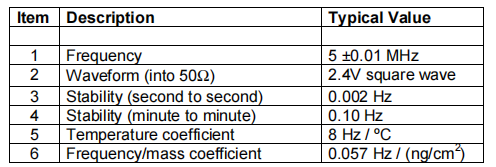
下表列出了来自 QCM 控制器的针对晶体在水中的频率信号的典型特征。

频率计数器的许多特性是由它的时基决定的：如果时基使频率改变 10ppm，那么结果值也会改变 10ppm。虽然计数器的时基的准确性不是特别重要，但时基的稳定性是至关重要的，因为时基的变化与晶体表面累积质量的变化难以区分。通常制造商会指*精度和老化，但不指*短期稳定性。在几乎所有的使用中，如果允许他们长时间的使用，短期稳定性将会改善。为了避免降低频率测量，时基稳定性应该优于 0.002Hz/5MHz 或 1：4·10 -10 (1s)。

计数器的速度/分辨率也很重要：在典型的 QCM 测量中，累积质量可以快速变化，并且希望在一秒间隔内以 1:10 -10 的分辨率进行频率测量，以免显着降低质量分辨率或增加测量噪声。在一秒钟的间隔内简单地计数频率输出的周期并不能提供比 1：5·10 6 更好的分辨率，因此需要一个更复杂的“计数器”架构。一个“倒数插值”计数器可以提供比每个门间隔±1 个周期更好的频率分辨率。

几乎所有的频率计数器都可以测量由 QCM 频率输出的 50Ω 中的 2.4Vpp 方波的频率。

计数器可与 RS-232 或 IEEE-488（或两者）通讯，以方便接口计数器与计算机进行数据采集。接口的速度不是很重要，因为通常每秒只读取一次。通过计算机接口进行设置和读取计数器相对简单。美国国家仪器实验室视图产品或其他数据采集程序的软件驱动程序通常是可用的。

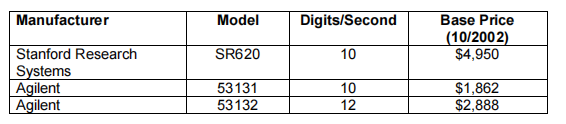
用于 SRS QCM 测量的频率计数器如下（2002 年 10 月价格）：

频率测量中的误差

QCM25 晶体控制器将在使整个环路的相移为 360°的频率上振荡。在环路中相位偏移的重要因素包括：

1.180°来自反相放大器 A 1 。

2.180°+[37°/ Hz 偏离 5MHz]来自低通滤波器。

3.0°+[0.20°/pF（R _m =40Ω）或 0.81°/pF（R _m =375Ω）]，来自未补偿的 Co。

4.0° + [0.20°/Hz (R _m =40) or 0.04°/Hz( R _m =375) 来自 R _s / R _m / R _L 环路中的晶体产生的串联谐振偏差。

如果存在额外的相移（#2 或#3），振荡器将远离串联谐振，从而使晶体环路（#4 上面）消除外来的相移。额外的相移值较小，加上晶体环路的 dφ/df 比较大，则使这些频率误差很小。

QCM25 晶体控制器仅适用于 5MHz 晶体。晶体频率的常规精度为 100ppm，或 500Hz。低通滤波器在从 5MHz 到 500Hz 时将增加额外的相移偏差 37°/ Hz x 500Hz=0.0185°，这将导致干晶体偏离串联谐振 0.0185°/0.20°/Hz=0.092Hz，或湿晶体偏离串联谐振 0.0185°/0.04°/Hz=0.462Hz。由于低通滤波器的 dφ/df 比湿晶体的 dφ/df 小 1000 倍，因此低通滤波器不会对串联谐振频率的测量产生显著的误差。

通过调制零值 C _o 的可变电容，并使用同步检测来定位*小增益操作点，QCM 允许用户重复地将零值 C _o 调到±0.01pF。相应的湿晶体相位误差为±0.01pF×0.81°/pF=±0.0081°，频率重现性为±0.0081°/0.04°/Hz=±0.20Hz。这个误差几乎是微不足道的了。

在水中，频率漂移的主要来源是液体粘度对温度的依赖性：在水中 5MHz AT-cut 晶体的串联谐振频率将增加约 8Hz/℃。

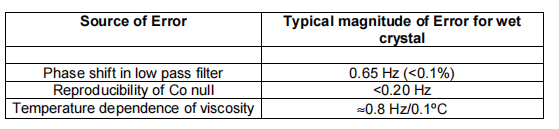
频率误差因素汇总（在水中，f=700Hz）

电阻测量

QCM 模拟控制器提供一个电导⁷ 电压输出(BNC 端口），这与晶体的运动串联谐振电阻有关：

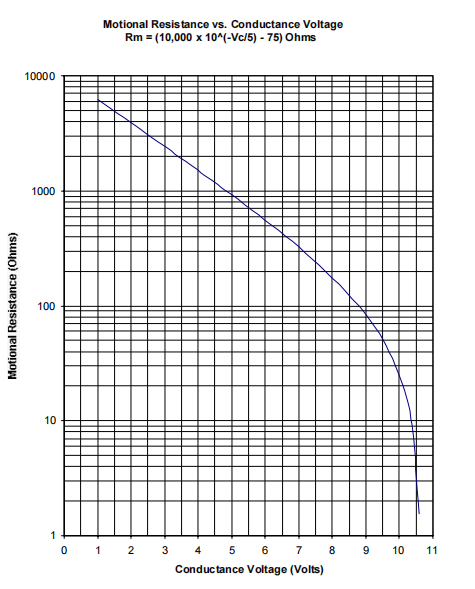
R _m =10000·10 ^-Vc/5 -75（equation 2），

其中，R _m 串联谐振运动电阻，以 Ω 为单位

V ^c 电导电压输出，以 V 为单位。

建议使用高精度数字电压表⁸ 进行测量，至少具有 6 位分辨率和计算机接口。

电阻计算

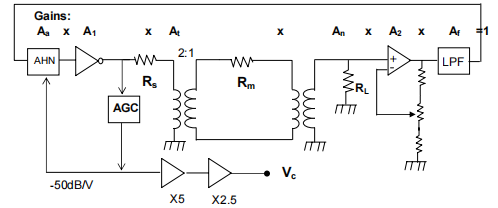
图 5. QCM 增益模型

QCM25 晶体控制器的增益模型如图 5 所示。在串联谐振时，晶体的运动电感和运动电容的电抗相互抵消，因此晶体可以仅用晶体的运动电阻 R _m 来表示。（还假设静电电容 C o 如前所述已为零）。如果有足够的增益来克服电路损耗，电路将在环路周围的净相移为 360°的频率上振荡。

模型中的两个电路提供了相移，反相放大器提供 180°的相移，低通滤波器调整为 5MHz 时提供了 180°的相移，因此，电路将在晶体具有电阻性的频率上振荡，即在串联谐振时振荡。

回路增益是每个电路器件的增益（或衰减）的乘积。如果回路增益恰好为 1，那么振荡振幅将保持在一个固定的水平，AGC 电路通过由电压控制的可变衰减器来控制回路的增益。

从左到右，该电路由以下几个部分组成：

1. 一种电压控制可变衰减器，衰减为 A _a 。自动增益控制电路产生电压，使振荡幅度在 1V _pp 的固定水平。衰减器由该电压控制，在 0 到 1V _dc 之间，提供 50dB/Volt 的衰减，使 A _a =10 ^{-Vagc· 50/20} 。AGC 电压在 QCM25 晶体控制器中放大 5 倍，在 QCM 模拟控制器中放大 2.5 倍，然后通过 QCM 前面板上的电导 BNC 输出。因此，QCM 电导输出 BNC 处的参考电压 V _c ，A a =10 ^-Vc/5 。

2. 一个固定增益放大器，增益为 A ₁ =45 dB+20log（250/200）=46.94 dB（或-222x）。该反相放大器的带宽为 500MHz，因此引入了的额外相移很小。

3. 100Ω 的源电阻 R s 。该源电阻由两个串联 50Ω 电阻组成，其中一个在放大器 A ₁ 内部。通过随后的 2:1 变压器，该源阻抗降低了 4 倍，至 25Ω。

4. 具有 2：1 匝数比的隔离变压器，因此衰减为 A _t =0.5x，该变压器允许晶体与振荡器电路的电流隔离，这在电化学应用中是很重要的。除了将源阻抗降低 4 倍外，变压器还将变压器输入端的负载阻抗增加 4 倍，因此当 R _m =0Ω 时，负载将为 200Ω。

5. R _m ，晶体在串联谐振时的运动电阻。R _m 的变化范围，干晶体的约为 10-40Ω，水中的晶体约为 375Ω，90%（w/w）甘油/水溶液中的约为 5kΩ。

6. 第二个隔离变压器，匝数比为 1：1，该变压器允许晶体与振荡器电路的电流隔离。

7. 负载电阻 R _L 为 50Ω。R _s 、R _m 和 R _L 的电路提供了一个回路衰减 A _n ，它取决于晶体的运动电阻。A _n = R _L /（R _s /4 + R _m + R _L ）。

8. 增益可调的射频放大器 A ₂ ，增益约为 4.43 倍。该放大器的增益 A ₂ 在校准期间设置，以补偿所有其他电路元件的增益变化。

9. 低通滤波器。该滤波器是一个 5 阶贝塞尔低通滤波器，f _c =3.7MHz，调整后可在 5MHz 时提供 180°的相移。该滤波器的相移，加上反相放大器 A ₁ 的 180°相移，一起提供了振荡所需的360°相移。低通滤波器需要抑制由于环路放大器的高带宽而产生的杂散振荡，低通滤波器在5MHz 时的信号衰减约 A _f =-7.8dB（或 0.407x）。

现在可以计算出晶体在串联谐振下的运动电阻。当电路以恒定的振幅振荡时，环路周围所有元件的增益（或衰减）的乘积就是 1。因此，

A _a · A ₁ · A _t · A _n · A ₂ · A _f = 1

重新排列并用方程代替 A _n ，

1 / A_n= ( R _s /4 + R _m + R_L) / R _L = A _a · (A ₁ · A _t · A ₂ · A _f )

求解 R_m，

R _m = R _L · A _a · (A ₁ · A _t · A ₂ · A _f ) – R _L – R _s / 4

从上述电压衰减器的特性来看，A _a = 10 ^-Vc/5 ，其中 V _c 是在 QCM 上电导输出 BNC 处的电压。在工厂校准时调整 A ₂ ，使增益（A ₁ ·A _t ·A ₂ ·A _f ）= 200。所以我们得出，

R _m = 10,000·10 ^-Vc/5 -75，

其中，

R _{m -}运动串联谐振电阻，以 Ω 为单位

V _{c -}电导电压输出，以 V 为单位。

晶体在串联谐振时的运动电阻 R _m 可有上式计算。见下图 6， R _m vs.V _c ：

图 6.运动串联谐振电阻与电导电压的关系

R _m 的测量误差

R _m 的测量误差将小于 R _m 的 3Ω +3%（其中 R _m < 2kΩ），并且主要由变压衰减器偏离其标称(电压，增益)特性。

还要记住，液体和软膜中的电阻测量也受到温度的影响，主要是通过粘度的温度系数。例如，在室温附近的水中，电阻预计会出现 4Ω/°C 的漂移。

R m 测量中的噪声

V _c 在大多数情况下与 R _m 呈对数变化。这样做有一个重要的优势：电阻的分数分辨率几乎与电阻无关，因此可以对粘性损耗进行详细和低噪声的测量。为了估计电阻测量中的噪声，我们可以对运动电阻的方程求导（单位为欧姆和欧姆/伏特）：

R _m = (10,000 ·10 ^-Vc/5 -75)

dR _m / dV _c = 10,000 · 10 ^–Vc/5 · ln (10) · (-1/5)

= -2,000 · ln (10) · 10 ^–Vc/5

≈ -4605 · 10 ^–Vc/5

≈ -0.4605 · (R _m + 75)

V _c 信号上的噪声V _c 通常是±50V（平均 1 秒的时候）。水中 5MHz 晶体的 R _m 约为 375Ω。则电阻测量中的分数噪声为：

R _m /R _m = V _c · [dR _m / dV _c ] / R _m = V _c · [-0.4605 · (R _m + 75)] / R _m = ± 28 ppm.

这种低底噪的分数电阻测量允许非常小的损耗变化。这也是为什么对这些测量建议使用高精度电压表（即至少有 6 位分辨率）的原因。

R _m 的校准

QCM25 晶体控制器/QCM 主机的电阻测量是通过将晶体替换为与 15pF 电容并联的精密电阻来校准的。使用了两个电阻值：51.10Ω 和 1.000kΩ。R _m 的方程可以倒置以确定 V _c 的校准值。（运动电阻 R _m ，单位为 Ω，电导电压输出 V _c ，单位为伏特。）

R_m= (10,000 10 ^-Vc/5 - 75)

V _c = 5 log [ 10,000 / (R _m + 75) ]

调整低通滤波器，使 QCM25 晶体控制器以 5MHz 振荡，并用 51.10Ω 电阻代替晶体。调整变容体表盘，使晶体控制器振荡在 5MHz 与 1.000kΩ 电阻代替晶体的地方。调整 QCM25 晶体控制器中的校准电位器，使 V _c = 9.496V _dc ，校准电阻为 51.10Ω，并使 V _c = 4.843V _dc ，校准电阻为 1.000kΩ。

气相测量

QCM 的*次应用是作为气相、薄膜沉积中的质量传感器和厚度监测器。到目前为止，该技术仍然是*重要的应用领域之一。

Sauerbrey 方程

Sauerbrey 方程（equation 1）常用于计算真空沉积过程中的质量荷载和薄膜厚度。基本假设是，外膜质量的增量变化被视为是底层石英厚度的延伸，外膜被认为是刚性且薄的，在振动过程中不会受到任何剪切力的影响。因此，灵敏度因子 C _f 是石英晶体的基本性质，而不考虑外膜的任何性质（即它只依赖于石英的声弹性）。

C _f = 2 . n . f _o ² /(ρ_q .∝ _q ) ^1/2 (equation 3)

其中，

n - 驱动晶体的谐波数,

f _o -晶体基模的谐振频率，单位为 Hz,

ρ _q - 石英的密度为-2.648gcm ^-3 ，和

_μq- 石英剪切模量- 2.947 . 10 ¹¹ g . cm ^-1 . s ^-2

频率变化对单位面积质量覆盖的依赖性，强调了这样一个事实，即在一定范围内，灵敏度因子与电极几何形状无关。因此，在理论上，QCM 质量传感器不需要为此进行校准。这种从*一性原理计算质量载荷的能力显然是这些设备的一个非常活跃的特性。

薄膜厚度通常是气相薄膜沉积中一个重要的参数。如果质量覆盖被认为是均匀的，那么薄膜的厚度便能很容易地计算出来，用 Sauerbrey 方程提供的单位面积的质量除以材料的密度：

T _f = m / ρ _f      (equation 4)

其中，

ρ _f - 薄膜材料密度, in g/cm ³ ,

m - 每单位面积质量的变化，in g/cm ² (calculated from Sauerbrey’s equation), and

T ^f -薄膜的厚度，in cm。

Z 匹配法

一般认为，当沉积物的质量载荷引起的频率变化小于空载晶体频率的 2%时，可以使用 Sauerbrey方程来计算薄膜厚度的准确结果⁹ 。随着薄膜厚度的增加，必须扩展 Sauerbrey 方程，以纳入沉积物的弹性。Lu 和 Lewis ¹⁰ 给出了一个特别简单的方程（方程 5）来计算f 对m 的依赖性，目前大多数 QCM 用户都使用这个公式来计算气相沉积中刚性薄膜的厚度。

m = [(N_q .ρ _q )/(Π . Z . f _L )] . tan ^-1 [ Z . tan[Π . (f _U - f _L ) / f _U ]]     (equation 5)

其中，

m - 单位面积质量变化 in g/cm ² ,

N _q - AT-cut 石英晶体的频率常数： 1.668*1013 Hz. ,

ρ _q -石英密度： 2.648 g . cm ^-3 ,

ρ _f - 薄膜材料密度, in g . cm ^-3 ,

f _U - 空载晶体频率（沉积前）, in Hz,

f _L - 负载晶体的频率, in Hz,

_μq-石英剪切模量: 2.947 . 10 ¹¹ g . cm ^-1 . s ^-2 ,

_μf- 薄膜材料的剪切模量, and

Z: Z-Factor of film material = [(ρ _q . _μq ) / (ρ _f . _μf )] ^1/2 .

这种对频率变化的分析，包括石英和薄膜的声阻抗的分析，通常被称为“z 匹配”方法。质量载荷和薄膜厚度计算的精度通常受到 z 因子和材料密度的已知程度的限制。密度值和 z 因子值通常非常接近于体积值。常见薄膜材料的体积密度和剪切模量值可以在许多材料参考手册中找到。

一般认为，当频率变化高达 40%(相对于空载晶体)时，Lu 和 Lewis 方程与实验结果¹¹ 吻合得很好。还要记住，z 匹配方程严格适用于“刚性”沉积。表现为粘弹性的薄膜，如一些具有大厚度或粘度的有机聚合物薄膜，将表现出方程 1 和方程 5 的显著偏差。

晶体故障也经常在频率达到 40%移位之前出现。常见的问题有：(1)由于过度沉积而导致晶体电极短路，(2)由于复合谐振模式的累积而导致其他（非谐波）谐振频率，(3)由于电极和薄膜之间形成的边缘电极场而偏离理论结果，(4)由于晶体表面应力积累而导致基频的意外变化，(5)由于源材料的飞溅而导致薄膜不均匀等。

液体测量

直到*近，人们还认为，禁止在过多的粘性载荷的液体中使用 QCM。事实上，在液体中操作确实是有可能的，并且 QCM 的响应对固体溶液界面的质量变化依旧非常敏感。多年来，QCM 一直被用于与液体和/或粘弹性薄膜的直接接触，以评估化学和电化学表面过程中质量和粘弹性性能的变化。

当 QCM 与溶液接触时，频率就会下降，这取决于溶液的粘度和密度。正确地解释在全液体浸入条件下的实验结果的先决条件是对谐振腔进行定量。这个问题首先由 Glassford 1³ 发现，后来由Kanazawa 和 Gordon ¹⁴ 解决。
Kanazawa 解决了溶液性质对晶体的影响（方程 6），可以预测晶体浸入粘性介质时共振频率的变化：
f = - fu^3/2 . [(ρ_L .η _L )/ (Π . ρ _q . _μq )] ^1/2 (equation 6)
其中，
f _{u -} 空载晶体的振荡频率，
ρ _{q -} 石英密度 – 2.648 g . cm ^-3 ,
_μq- 石英剪切模量- 2.947 . 10 ¹¹ g . cm ^-1 . s ^-2 ,
ρ _{L -} 与电极接触的液体的密度，
η _{L -} 与电极接触的液体的粘度。
液体介质与振荡晶体表面的粘性耦合不仅导致串联谐振频率降低，而且还导致谐振振荡的阻尼减小——粘性损耗表现为 QCM 谐振器的串联谐振电阻 R 的增加。因此，R 可以作为晶体表面与介质（即液体或软薄膜）的粘性载荷之间一个极好的独立指标。
在溶液¹⁵的化学和电化学沉积过程中，f 和R 测量都通常作为 QCM 谐振器晶体-液体界面的质量载荷和粘度的独立指标。
在另一项研究¹⁶ 中，应用 Butterworth-Van Dyke 等效电路模型（图 1）推导了石英振荡器的串联谐振电阻的变化R 与(ρ _L ·η _L ) ^1/2 液体载荷之间的线性关系：
R = [n . ω_s .L _u / Π] . [ (2 . ω_s .ρ _L . η _L )/ (ρ _q . _μq )] ^1/2 (equation 7)
其中，
R - 串联谐振电阻的变化, 为单位,
n - 与液体接触的边数，
ω _{s -} 串联谐振时的角频率(= 2 . Π . f _s , 其中 f _s 是在溶液中的振荡频率，Hz 为单位),
L _{u -}无干扰的谐振器电感 (即干燥条件下) 通常以 mH 为单位.
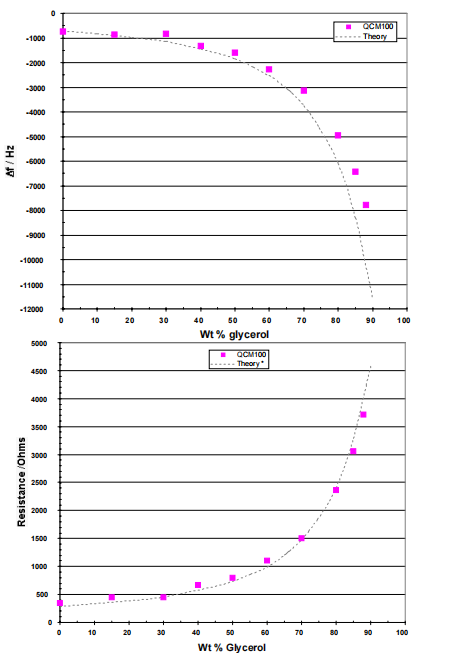
QCM 系统是专门为了在高粘性载荷下的操作而设计的。标准晶体 holder 支持在气体和液体环境中操作，并为了满足电化学 QCM 测量的兼容性要求，提供了暴露于液体的单电极¹⁷ （即方程 7 中的n=1）。QCM25 晶体控制器提供频率和电阻变化信号，并将振荡保持在约 5 KΩ 的串联谐振电阻（即，它将支持晶体运行在高达 88%甘油/水的高粘性溶液中）。

图 7.f 和R 与甘油重量百分比（在水中）的关系，用 QCM 和 5MHz 抛光晶体测量的理论预测。

例如，方程 6 预测在 20°C 下，从真空转移到纯水¹⁸ 时，f ₀ 下降了 715Hz，这与 QCM 使用直径1 英寸的抛光 5MHz 晶体安装在标准晶体 holder 上所观察到的结果一致。频率和电阻方程与实验结果非常吻合¹⁹ ，使 QCM 成为评价流体性能的很好的工具。应用实例包括对润滑油和石油性能的现场监测²⁰ 。清楚地说明了理论（方程 6 和 7）与实验之间的紧密对应关系，如图 7。

耗散技术
另一种研究负载 QCM 传感器特性的方法²¹，称为“耗散技术”，已被用于气体和液体环境中。在这种情况下，晶体以其谐振频率驱动，该振荡器可以间歇地断开，导致晶体振荡振幅呈指数衰减。从记录的衰减曲线中，可以同时得到绝对 Q 因子（与 R 成反比）和振荡器的频率。独立研究²²表明，只要寄生电容（C ₀ ）的影响被适当地消除，耗散技术提供的结果应该与 QCM 提供的测量结果具有一致性。

温度
石英晶体的谐振频率对温度的固有依赖性是众所周知的，而且通常都很小。事实上，QCM 实验中常用的 AT-cut 石英晶体的在室温下的系数接近于零。因此，在室温（≈1-3Hz/°C）左右，QCM 传感器晶体的固有依赖性可以忽略不计，在气相的单层吸附/解吸过程中通常被忽略。
当 QCM 晶体浸入液体中时，频率受温度的影响会有更大的变化。这是由于切变模式振荡与流体的温度依赖性粘度和密度的耦合——由于这种影响的温度系数为≈8Hz/°C 在水中。因此，对于要长时间监测频率的液相实验中，温度必须控制在至少 0.1°C，而且尽可能的更低。在电化学实验中，这通常是通过温度控制的缸体和夹套电池来实现的。如果温度是不可控制的，在晶体与新介质接触后，至少等待 30 分钟再进行精确测量，并在试验期间测量晶体周围溶液的温度，以进行温度补偿，这是很好的方法。同样常见的做法是，在进行任何实验之前，将已安装的晶体浸泡在溶液中过夜，以确保更稳定的读数。
在高精度测量中需要仔细控制温度，以避免频率滞后效应——在特定温度下的谐振器频率依赖于谐振器先前的温度。例如，通常观察到从 T1 到 T2 得到的频率与温度曲线与立即从 T2 到 T1 得到的温度曲线并不一致。在进行精准测量时，必须仔细考虑这种影响。
每位 QCM 用户必须确定温度对正在进行的实验的影响，并相应地控制温度，或者测量温度并对其进行补偿。

电极抛光
由于液体被困在晶体表面的孔隙中，所以电极表面粗糙度会引起较大的表观质量负荷²³ 。一般情况下，在液体浸没实验中，需要光学抛光晶体（50 平均表面粗糙度）以便获得理论和实验之间良好的一致性。水浸检查测试（如下）提供了一种快速方便的方法来测试用于液体 QCM 应用的晶体表面光洁度。
 

系统检查
当用 QCM 进行一种新的液体测试时，与方程 6（和方程 7）的理论预测进行比较通常是一个很好的起点。本文描述了两种常见的“检查”程序：
水浸：对于用 5Mhz 抛光晶体，假设电极电容被适当消除，当从空气中完全切换到浸入 20℃的水中的话，频率降低≈715Hz，串联谐振电阻增加≈380Ω。
甘油/水浸没：图 7 显示了在 20C 条件下的一系列粘性甘油/水溶液中浸泡的抛光 5MHz 晶体的电阻和频率变化值。在增加甘油浓度下操作是 QCM 实验装置的一个很好的测试，并且应该提供高达88%以上的甘油的可预测的结果。
在这两种方法中，对于甘油浓度高达 70%时，在期望值和测量值之间 的一致性在±25%以内通常被认为是可以接受的。
对于未抛光的晶体，频率位移要大得多（至少两倍）并且不可预测，因此不推荐用于系统检查。

电化学石英晶体微天平
在大多数电化学实验中，当材料从“工作”电极上沉积或丢失时，质量就会发生变化。与电化学响应同时监测这些变化是很有意义的，而 QCM 是这样做的标准方法。作为一种重量探针，QCM 已被用于许多类型的电化学研究，包括：金属的欠电势沉积²⁴ 、腐蚀、氧化物的形成、溶解研究 ²⁵ 、表面活性剂的吸附/解吸²⁶ 和导电聚合物薄膜在氧化还原过程中的变化 ²⁷ 。
QCM 在电化学过程中的基本原理和应用已经在电化学文献²⁸ 中得到了广泛的综述，在本手册中只进行简要的讨论。有关更多详细信息，请参考本章末尾的出版物列表。

电化学装置
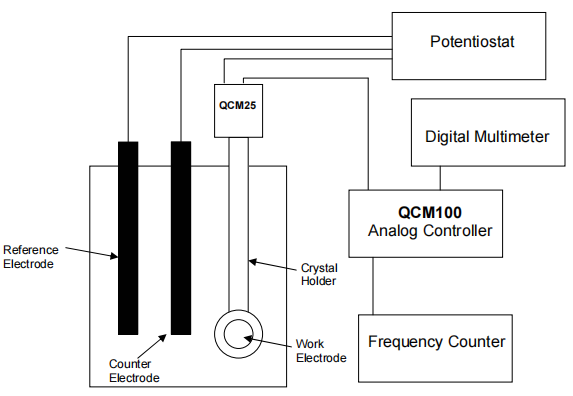
电化学石英晶体微平衡（EQCM）实验装置示意图如图 8 所示。在这个例子中，一个直径为 1 英寸的抛光 QCM 晶体被安装在晶体支架上，只有一个电极暴露在导电溶液中。晶体支架连接到 QCM25晶体控制器上，液体接触电极连接到恒电位器的“工作电极”引线（通过 QCM25 晶体控制器的“晶体面偏置”连接器）。QCM200 模拟控制器提供独立的频率和电导输出，这些输出分别由频率计数器和数字万用表（或 A/D 转换器）读取和显示。

图 8.EQCM 设备的示意图

PC（图中未显示）通常与恒电位器、频率计数器和 DMM 接口，并将 QCM 和电化学数据集成到一个单一的软件包中。
注：QCM25 晶体控制器提供了晶体正面电极的变压器隔离。这使得石英晶体面可以直接电连到任何标准恒电位器/恒流器的“工作电极”引脚。
图 8 中的仪器，一个典型的循环伏安 EQCM 实验将涉及应用到电化学波形工作电极上，同时测量通过电化学电池的电流和晶体的振荡频率和串联谐振电阻。
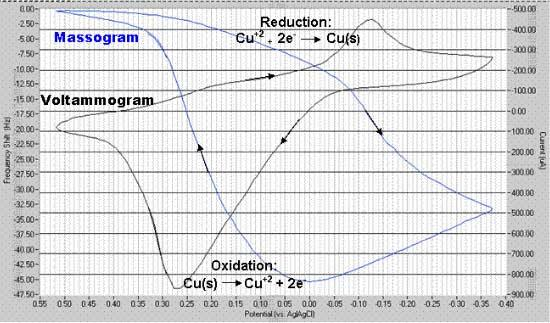
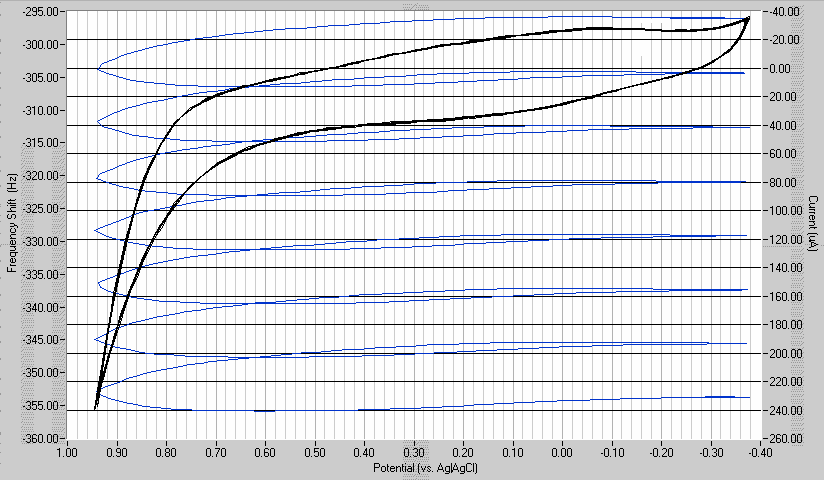
图 9 是一个典型的伏安图-质量图的例子，从 10mM 硫酸铜溶液中获得 0.1M 的硫酸，使用直径1 英寸的镀金石英晶体安装在标准支架作为工作电极。

图 9.在 Au 电极上沉积铜的循环伏安图和质量图数据。

频率-势图显示，随着铜金属在晶体表面的沉积，频率下降完全同步。

校准
文献已经充分证明，当实验只涉及在固定溶液中测量的相对频率转移时，有液体粘性载荷引起的偏移对用于确定刚性沉积物中质量变化的 Sauerbrey 方程的准确性的影响可以忽略不计²⁹ 。在这些情况下，EQCM 数据的定量解释是基于 Sauerbrey 方程（方程 1）和法拉第定律的结合。前者将频率的变化与薄且坚硬的沉积物的质量变化联系起来，而后者将电化学实验中通过的电荷与电解材料的摩尔数联系起来。因此，频率的变化与通过的总电荷有关。
一个例子是银在 QCM 的铂电极晶体上的电沉积。电荷 Q 是还原过程中在界面上传递的电子总数的积分度量。在某种程度上，如果每提供一个电子都会导致一个 Ag 原子的沉积，那么 Q 和f 之间应该存在线性关系，如方程 8 所示：
f = 10 ⁶ . M ^w . C ^f . Q / (n . F . A) （equations 8）
其中，
f - 频率变化, 单位 Hz,
M _{w -} 沉积物种的表观摩尔质量,单位 grams/mole,
C _{f -} Sauerbrey 对所用晶体的灵敏度因子（见方程 1），
Q - 在减少过程中产生的综合电荷, 单位 Coulomb,
A - 工作（即液体接触）电极的活性沉积区域, 单位 cm ² ,
F - 法拉第常数： 9.648 .10 ⁴ 库仑/摩尔,
n - 转移到诱导沉积的电子数(i.e. n =1 for Ag deposition).
(10 ⁶ 提供了从 C _f 中的 mg 到 M _w 中的 g 的单位转换)
当考虑到 n 时，“f vs Q”的图将给出沉积物质的每个电子的表观质量。这通常被用来阐明伴随氧化还原过程的质量变化，因此对表征电子转移反应的机制非常有用。
然而，在根据方程 8 进行任何计算之前，必须校准 EQCM，以便正确地推导(1)溶液中Sauerbrey 方程的比例常数 Cf，(2)考虑工作电极的有效面积。这通常是通过良好的电化学反应来完成的——通常是将银、铜或铅电沉积在金或铂电极上。
斯坦福厂家青睐的对 QCM200 系统的 EQCM 校准方法是基于 Ag 的恒流沉积：50mM 硝酸银溶液置于 0.5M 的硝酸中，受到还原电位的作用，Ag 以 50-500A/cm 2 的固定阴极电流密度沉积。将阴极电流进行积分，得到电荷随时间的函数。在 1g/cm ² 范围内的沉积，通常在“f vs Q”图中观察到良好的线性，这是用于校准方程 8 的比例常数一种非常可靠的方法。
在电化学文献³⁰ 中也描述了几个校准程序，详情请参考本章末尾的出版物列表。

聚合物修饰电极
EQCM 已被广泛用于研究聚合物修饰电极，特别是作为一种跟踪氧化还原过程的重量测量工具³¹ 。然而，为了使线性频率-质量关系（由方程 8 描述）成立，聚合物覆盖层在电化学过程中必须不改变其刚性。否则，粘弹性的变化也会导致频率的变化，从而导致对质量变化的错误解释³² 。因此，在聚合物薄膜实验中，必须确定聚合物薄膜的粘弹性性能是否会影响频率的测量！

中₄0.1M 吡咯在 0.1M HCLO

图 10.吡咯氧化形成聚吡咯膜在金涂层 QCM 传感器晶体上的的伏安图和质量图数据。本实验采用-0.4~0.95V 范围内进行了 7 次伏安循环。吡咯单体在 0.65V 时可被氧化为自由基。当这种情况发生时，在晶体表面形成了一层薄薄的聚吡咯薄膜，导致晶体振荡的基频降低。扫描过程中频率的不可逆下降证明了薄膜的持续增长。

检测氧化还原膜粘弹性变化的一种直接方法是在电化学实验过程中同时监测石英振荡器的串联谐振电阻 R ³³ 。一些基于同时对f 和R 进行测量的理论模型³⁴ ，已经在文献中讨论了将 EQCM 重量测量扩展到非刚性薄膜的方法。由于剪切波同时存在于石英晶体、粘弹性膜和邻近溶液中，因此必须考虑剪切波的反射，因此 EQCM 体系中聚合物薄膜的粘弹性分析是复杂的。然而，解决这个问题是有价值的，特别是如果薄膜的材料性质可以被推导出来。这将使薄膜的电化学行为与其材料性质相关联³⁵ 。
QCM 技术的独特之处在于它能够确定非常薄的薄膜质量，同时提供关于其粘弹性特性的信息。测量质量和结构变化的能力意味着它可以检测到聚合物薄膜中的相变、交联和膨胀³⁶ 。

化学和生物传感器
任何有质量的东西都可以在 QCM 传感器上产生响应。该装置可以普遍的响应是该技术得到广泛应用的原因。然而，这种普遍的缺点是敏感性，会使实验总是有很多的干扰。为了进行分析，必须找到一些方法，让 QCM 传感器只对您感兴趣的东西做出响应（即在设备中构建灵敏度）。这通常涉及到在晶体³⁷ 的表面上添加一层敏感层。
有机聚合物是 QCM 传感器*常用的涂层，因为它们具有可逆吸附蒸汽和液体的能力³⁸ 。在许多关于使用聚合物涂层进行蒸汽传感的工作中，聚合物材料的声学性能都被忽视了。薄膜的质量载荷和粘弹性贡献对观察到的 QCM 响应的相对重要性是一个尚未解决的问题。
近年来，在生化分析领域，QCM 的应用从未有过如此戏剧性的增长。QCM 装置通常被用作生化和免疫学检测³⁹ ，以及用于调查和/或监测重要的生化过程。通过使用抗原抗体 ⁴⁰ 、酶底物和其他受体-蛋白对，可以实现对生物化学活性化合物的敏感性、选择性的检测。本文综述了这些材料的潜在分析用途，特别是在发展生化传感器方面⁴¹ 。QCM 研究为一系列生物芯片和生物传感器应用提供了功能化表面的详细信息。
QCM 被生物学家和生物化学家通常应用于获取有关过程的信息，例如： (1)蛋白质吸附/解吸⁴² ，(2)细胞粘附⁴³ ，(3)蛋白质-蛋白质相互作用，(4)聚合物的降解，(5)生物污染和生物膜的形成，(6)药物分析⁴⁴ 和(7) DNA 生物传感器 ⁴⁵ 。

参考文献
¹ G. Sauerbrey, Z. Phys. 155 (1959) 206
² Daniel Buttry, “Applications of the QCM to Electrochemistry”, in A Series of Advances in ElectroanalyticalChemistry, edited by Allen Bard, Marcel Dekker, 1991, p. 23-33.
³ John Henderson, “Electronic Devices. Concepts and Applications”, Prentice Hall, NJ, (1991) p. 357
⁴ For example, QCM10 crystal holder with a 1inch, 5MHz crystal, connected directly to an SRS QCM25 Crystal
Controller.
⁵ C. Chagnard, P. Gilbert, N. Watkins, T. Beeler and David W. Paul, “An electronic oscillator with automatic gain control:EQCM Applications”, Sensors and Actuators B 32(1996) 129-136. A. Arnau, T. Sogorb and Y. Jimenez, “Circuit for continuous motional series resonat frequency and motional resistance monitoring of quartz crystal resonators by parallel capacitance cancellation”, Rev. Sci. Instrum. 73(7)(2002) 2724.
⁶ For example, from the Conductance Output of the QCM100.
⁷ Conductance is the inverse of resistance: Conductance = 1 / Resistance or Resistance = 1 / Conductance. The units of resistance are Ohms [ = V/A] and the units of conductance are Siemens (S = A/V].
⁸ For example, Agilent 34401A, with 6 digit resolution or 3458, with eight digits resolution.
⁹ D.R. Denison, “Linearity of a Heavily Loaded Quartz Crystal Microbalance”, J. Vac.Sci. Technol. 10(1) (1973) 126 Klaus H. Behrndt, “Long Term Operation of Crystal Oscillators in Thin-Film Deposition”, J. Vac. Sci. technol. 8(5)(1971) 622.
¹⁰ C. Lu and O. Lewis, “Investigation of film-thickness determination by oscillating quartz resonators with largemass load”, J. Appl. Phys. 43 (1972) 4385. Chih-shun Lu, “Mass determination with piezoelectric quartz crystal resonators”, J. Vac. Sci Technol., 12(1) (1975) 578.
¹¹ D. R. Denison, “Linearity of Heavily Loaded Quartz Crystal Microbalance”, J. Vac.Sci. Technol. 10(1973) 126. K. H. Behrndt, “Long Term Operation of Crystal Oscillators in Thin-Film Deposition”,J. Vac. Sci. Technol. 8(5) (1971) 622.
¹² T. Nomura and M. Okuhara, Anal. Chim. Acta 142(1982) 281.
¹³ A. P. M. Glassford, “Response of a Quartz Crystal Microbalance to a liquid Deposit”, J. Vac. Sci. Technol.,15(6)(1978) 1836
¹⁴ K. Keiji Kanazawa and Joseph Gordon II, “Frequency of a Quartz Microbalance in Contact with Liquid”, Anal Chem. 57(1985) 1770 K. Keiji Kanazawa and Joseph G. Gordon II, Analytica Chimica Acta, 175(1985) 99-105.
¹⁵ Stephen J. Martin, James J. Spates, Kurt O. Wesendorf, thomas Schnneider and Robert J. Huber, “Resonator/Oscillator Response to Liquid Loading”, Anal Chem 69(1997) 2050.
¹⁶ Stephen Martin, Victoria Edwards Granstaff and Gregory C. Frye,“Characterization of a Quartz Crystal Microbalance with Simultaneous Mass and Liquid Loading”, Anal. Chem. 63 (1991) 2272.
¹⁷ Operation in liquids requires that the crystal be mounted in a holder such that only the front surface of the crystal is in contact with the fluid, while at the same time providing an electrical connection to both electrodes.
¹⁸ For pure water, at 20C, ρ L : 0.9982 g cm -3 , and η L : 1.002 . 10 -2 g cm -1 s -1 .
¹⁹ H. Muramatsu, Eiichi Tamiya and Isao Karube, “Computation of Equivalent Circuit Parameters of Quartz Crystals in Contact with Liquids and Study of Liquid Properties”, Anal. Chem. 60(1988) 2142 S.J. Geelhood, C. W. Frank and K. Kanazawa, “Transient Quartz Crystal Microbalance Behaviors Compared”, Journal of the Electrochemical Society, 149(2002) H33-H38. Mengsu Yang and Michael Thompson,“Multiple Chemical Information from the Thickness Shear Mode Acoustic Wave Sensor in the liquid Phase”, Anal.Chem. 65(1993) 1158
²⁰ S. J. Martin, R. W. Cernosek and J.J. Spates, “Sensing Liquid Properties with Shear mode Resonator Sensors”, in Proceeds from Transducers/Eurosensors IX, Stockholm, Sweden (1995)
²¹ Michael Rodahl, Fredrik Hook, Anatol Krozer, Peter Brzezinski and Bengt Kasemo, “QCM setup for frequency and Q-factor measurements in gaseous and liquid environments”, Rev. Sci. Instrum. 66(7)(1995)3924.
²² S. J. Geelhood, C.W. Frank and K. Kanazawa, “Transient QCM Behaviors Compared”, J. of theElectrochemical Society”, 149(1)(2002)H33
²³ Stephen Martin, et. al. ,”Effect of Surface Roughness on the Response of ThicknessShear Mode Resonators in Liquids”, Anal. Chem., 65(1993)2910. Michael Ward and Edward J. Delawski, “Radial Mass Sensitivity of the Quartz Crystal Microbalance in Liquid Media”, Anal. Chem. 63(1991) 886.
²⁴ Mark R. Deakin and Owen Melroy, “Underpotential Metal Deposition on Au, monitorred in situ with a Quartz Microbalance”, J. Electroanal. Chem. 239(1988) 321 Melroy, K. Kanazawa, J.G. Gordon II and D. Buttry, “Direct Determination of the Mass of an Underpotentially Deposited Monolayer of Lead on Gold”, Langmuir 2(1986)697. Masahiro Seo, Masaki Aomi and Kengo Yoshida, “A combined Piezoelectric and EQCM study of Underpotential Deposition of Silver on Gold Electrodes”, Electrochimica Acta, 39(8/9) (1994) 1039 Youngran Lim and Euijin Hwang, “An Electrochemical QCM study of Oxygen reducttion during the Underpotential Depoosition of Lead on a Gold Electrode”, Bull. Korean Chem Soc. 17(12)(1996)1091.
²⁵ EQCM/Wall Jet Split-Ring Disk Electrode study on Copper dissolution in Chloride Aqueous solution”, Anal. Sciences,16(2000)1049 Michael Benje, Matthias Eiermann, Udo Pittermann and Konrad G. Weil, “An improved Quartz Microbalnce. Applications to Electrocrystallizatuion and dissolution of Niquel”, Ber. Bunsenges, Phys. Chem. 90(1986) 435.
²⁶ Jorg Auge, Peter Hauptmann, Frank Eichelbaum and Stephen Rosler, “QCM sensor in liquids”, Sensors and Actuators B, 18-19 (1994) 518.
²⁷ Adrian W. Bott, “Characterization of Films Immobilized on an Electrode Surface Using the EQCM”, Current Separations 18:3(1999)79.

²⁸ Mark Deakin and Daniel Buttry, “Electrochemical Applications of the Quartz Crystal Microbalance”, Anal Chem, 61(20)(1989)183 Daniel Buttry and Michael Ward, “Measurement of Interfacial Processes at electrode surfaces with the EQCM”, Chem. Rev. 92(6) (1992) 1355

²⁹ Wolfgang Stockel and Rolf Schumacher, “In situ Microweighing at the Junction Metal/Electrolyte”, Ber. Bunsenges. Phys. Chem. 91(1987)345.
³⁰ C. Gabrielli , M. Keddam and R. Torrei., “Calibration of the Electrochemical Quartz Crystal Microbalance”, J. Electrochem. Soc. 139(9) (1991) 2657. Note: A calibration procedure based on the deposition of Ag on Au electrodes is described. Graeme Andrew Snook, "Investigation of Solid-State Reactions by Electrochemical and Quartz Crystal Microbalance Measurements" Ph.D. Thesis, 2000, Department of Chemistry, Monash University, Clayton 3168, Melbourne, Australia and Division of Minerals, CSIRO, Clayton South 3169 Melbourne, Australia, under the supervision of Professor Alan Maxwell Bond (Monash) and Professor Stephen Fletcher (CSIRO).Available for download from:http://www-bond.chem.monash.edu.au/theses/ Note: the use of Lead acetate is proposed as a better alternative to Cu and Ag deposition. Bruckenstein S. and Shay M., “Experimental aspects of use of the quartz crystal microbalance in solution”, Electrochim. Acta 30(1985) 1295
³¹ Duke Orata and Daniel A. Buttry, “Determination of Ion Populations and Solvent Content as fucntions of Redox State and pH in Polyaniline”, J. Am. Chem. Soc. 109(1987)3574.
³² Michael Ward, “Investigation of Open Circuit Reactions of Polymer Films Using the QCM. Reactions of Polyvinylferrocene Films”, J. Phys. Chem. 92(1988)2049. Charles K. Baker and John R. Reynolds, “A quartz microbalance study of the electrosynthesis of polypyrrole”, J. Electroanal Chem, 251(1988) 307.
³³ Stephen Martin, Victoria Edwards Granstaff and Gregory C. Frye, “Characterization of a Quartz Crystal Microbalance with Simultaneouus Mass and Liquid Loading”, Anal. Chem. 63 (1991) 2272. Ralf Lucklum and Peter Hauptmann, “The Df-DR QCM technique: an approach to an advanced sensor signal interpretation”, Electrochimica Acta, 45(2000) 3907.
³⁴ R.A. Etchenique and E. L. Calvo,”Gravimetric measurement in redox polymer electrodes with the EQCM beyond the Sauerbrey limit”, Electrochemistry Communications, 1(5)(1999)167. R.A.Etchenique and E. J. Calvo, “Electrochemical Quartz Crystal Impedance Study of Redox Hydrogel Mediators for Amperometryic Enzyme Electrodes”, Anal. Chem. 69(1997)4833.
³⁵ E. J. Calvo , R. Etchenique, P. N. Bartlett, K. Singhal and Santamaria, “Quartz Crystal Impedance studies at 10MHz of viscoelastic liquids and films”, Faraday Discuss.,107(1997)141. Diethelm Johannsmann, “Viscoelastic Analysis of Organic Thin Films” on quartz resonators”, Macromol. Chem. Phys. 200(1999)501.
³⁶ C. E. Reed, K. Keiji Kanazawa and J. Kaufman, “Physical description of a viscoelastica
³⁷ D. S. Ballantine, R. M. W